Dimensionering Flöden

// INTE FÄRDIGT //

Magasinering (fördröjningsmagasing, utjämningsmagasin etc) i ett makadamdike

Magasinvolym=Volym x porositet

TotalVolym ex. 300 m3, fylld med makadam (blandade fraktioner, ex. 8-16 mm sten, grus)

porositet ex. Makadam = 40% (dvs. 40 % hålrum där vatten kan finnas)

Magasinvolym = 300 x 0.6 => 180 m3 eller 180.000 liter.

Flöde dike

kanal med lutning Sb= 5 o/oo

botten 1 m

släntlutning 1:2

material grus

Q=Sb^1/2 * An * M * Rn^2/3

Sb=5/1000 => 0,005

M(mannings) = 30

An=1,0yn

Den hydrauliska radien R är definerad som tvärsnittets area, A, delad med tvärsnittets våta perimeter, P , dvs.längden av kontaktytan mellan kanalens väggar och vätskan

R =A/P    R=1/2 = 0.5

Porstorlek

Generellt gäller att ju större markporer, desto större vattengenomsläpplighet

Hydraulisk konduktivitet kan ses som ett mått på hur fort vatten kan röra sig igenom material

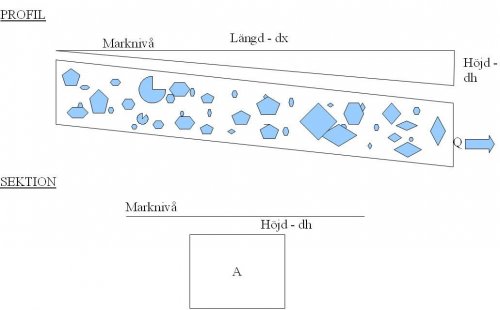
Dimensionera flöden i grundvatten makadamdike

Darcys ekvation för grundvattenflöde:

För att beräkna hur mycket vatten som passerar ett visst tvärsnitt genom marken använder man sig av Darcys lag. Lagen säger att grundvatten flödar snabbare ju högre permeabilitet ett lager har och ju mer grundvattenytan lutar. I ekvationsform blir lagen

Darcy´s flöde  Q = K · A · (dh/dx)          (m3/s)

K-Värde = Hydraulisk konduktivitet (m/s) För olika värden på K-värde, Porositet etc. Se Tabeller

Med hydraulisk konduktivitet avses en jord- eller bergarts materialspecifika förmåga att släppa igenom vatten, angiven som grundvattenflöde per tidsenhet. Då hänsyn tas till vätskans egenskaper (tätheten, temperaturen/viskositeten)
exempel K-värde Grus = (fraktion 2-60mm), 0.004

A = Area (se sektion), Tvärsnittsarea.

exempel 3 m2

dh/dx = sjunkning / längd, i meter
exemel 0.5 meter / 10 meter = 0,05    m/m

Q=0,004*3*0,05 => 0,006 m3/s => 0,6 l/s

Darcys - Vattenföring

Q = K(h/d)A

Q = grundvattenföringen (m3/s)
K = hydraulisk konduktivitet (m/s)
h/d = hydraulisk gradient = (h1-h2)/(x1-x2)
h = grundvattennivå (m) 
x = sträcka (m) 
A= tvärsnittsarea (m2)

Ekvationen ovan ger alltså vattenföringen, eller flödet, i kubikmeter per sekund. För att räkna ut medelhastigheten vd (m/s) över tvärsnittsaren A (m2), måste flödet Q delas med A, d.v.s:

Darcy-hastigheten

Darcy´s hastighet  q = Q/A      (m/s) 

vd=Q/A= K (h/d)

där medelhastigheten vd brukar benämnas Darcy-hastigheten. Observera att denna Darcy-hastighet faktiskt skiljer sig från en vattenpartikels medelhastighet. Det beror på att vattenpartiklarna inte flödar genom hela tvärsnittsarean A, eftersom en stor andel av denna area blockeras av jordpartiklar. Hur mycket plats som finns tillgänglig för vattenflöde trots denna blockering ges av jordens eller bergets porositet p, d.v.s. volymen porer delat med den totala jord- eller bergsvolymen. Porositeten är alltid mindre än ett men större än noll, och ligger t.ex. i allmänhet kring 0,3 för sand. Med hänsyn till denna blockering ges vattenpartiklarnas faktiska medelhastighet av sambandet:

vp= vd/p

där p som tidigare nämnts är jordens eller bergets porositet.

Verklig hastighet   v = q/Φ = (K · dh/dx)/Φ (m/s)

v=hastihet m/s  (genomsnittlig vattenhasighet)

Φ=Porositet Se Tabeller Grus = 0,28

q= se ovan, Darcys hastighet = 0,002   =>  0,00714

(K · dh/dx)/Φ (m/s) => 0,00714 m/s

Strömningen i grova stenfyllningar är turbulent
Den hydrauliska konduktiviteten räknas om till turbulenta hydrauliska konduktiviteten

Kt=1/β0 x n3/(1-n) x g x dt

Kt = turbulent hydraulisk konduktivitet (m/s)
β0 = formfaktor (= 3,6 för sprängsten) 
n = porositet i fyllningen 
g = borde vara gravitationen ca. 2 x π  ca. 9,82 m/s² (ej bekräftat)
dt = stenfördelningen, beräknas som dt = 1,7·d10
d10 = siktdiameter där 10 % av massan passerar

Kt=

1/3,6 =>0,278

0,4*3/ (1-0,4) => 1,2 / 0,6 => 2

x g

x 1,7*100=>170

Enkelkorniga jordarter

Då markporernas storlek är proportionell mot kornstorleken, får sandjordar och grovmojordar ofta en god vattengenomsläpplighet. Mjälajordar får däremot ofta en låg vattengenomsläpplighet.

För kornfraktioner i renbestånd kan vattengenomsläppligheten beräknas med den förenklade ekvationen K = 5 D² där

• K = markens vattengenomsläpplighet (m/s)
• D = korndiameter (m)

Exempel K=5 x 100^2  = 50000  (100 mm block)

Flödeshastighet i dike, Mannings formel

källa wikipedia 

Manningstal M = 45  (Grusyta)

S0 = Dikesbottens lutning (m/m) S0=0,05

B = dikesbredd (m) = 1 meter

y = Vattendjupet i diket (m) = 2 meter